Automatic Question Solving for Intelligent Tutoring
From a scientific point of view, developing automatic solvers for solving math (exercise) problems is an important indicator problem in artificial intelligence because solving math problems is the basic intelligence ability of human being and is the base of many other intelligent abilities. Meanwhile, the technology in automatic solving can greatly enhance the intelligence of tutoring systems for basic education. The research on solving math problems aims to develop algorithms that take a math problem described in natural language (and also in diagram) as input and output the solution of the input problem for the target math areas in basic education. The automatically generated humanoid solution is promising for the step-by-step tutoring of learners, and hhence has widely educational applications, such as AI-Tutor, automatic marking, and educational robots.
To this end, I have proposed a general framework and several models for automatically solving math (especially plane geometry) problems, for the aim of generating humanoid math tutoring.
The general framework
This is a relation extraction based general framework for automatic question solving. I divide this task into three steps: first I extract domain knowledge and generate the frequent linguistic patterns from large numbers of corpus. And then use this knowledge to guide the relation extraction and conduct deductive reasoning to generate the tutoring solutions. Specifically, we conduct text and diagram understanding simultaneously to transform the question into machine-understandable logics to generate the step-by-step tutoring.
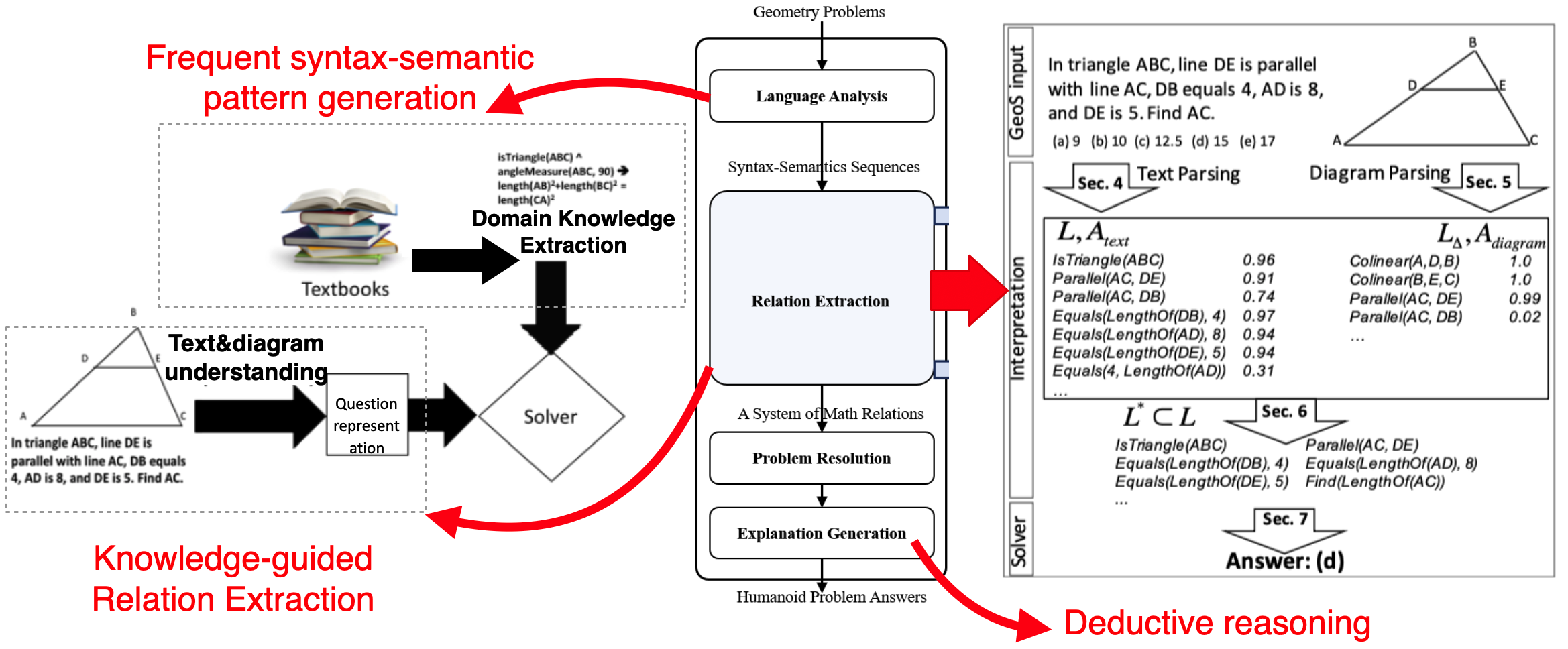
Xinguo Yu, Mingshu Wang, Wenbin Gan*, Bin He, and Nan Ye. A framework for solving explicit arithmetic word problems and proving plane geometry theorems, International Journal of Pattern Recognition and Artificial Intelligence, volume 33, page 1940005. World Scientific, 2019.
Xinguo Yu, Wenbin Gan, and Mingshu Wang. Understanding explicit arithmetic word problems and explicit plane geometry problems using syntax-semantics models. In 2017 International Conference on Asian Language Processing (IALP), pages 247–251. IEEE, 2017.
Xinguo Yu, Danfeng Yang, Wan Ding, and Wenbin Gan. Preliminary research and development on the problem-solving humanoid machine for k-12 education. In 2014 International Conference of Educational Innovation through Technology (EITT), pages 99–104. IEEE, 2014.
Based on this framework, I have proposed several methods to solve different kinds of math problems.
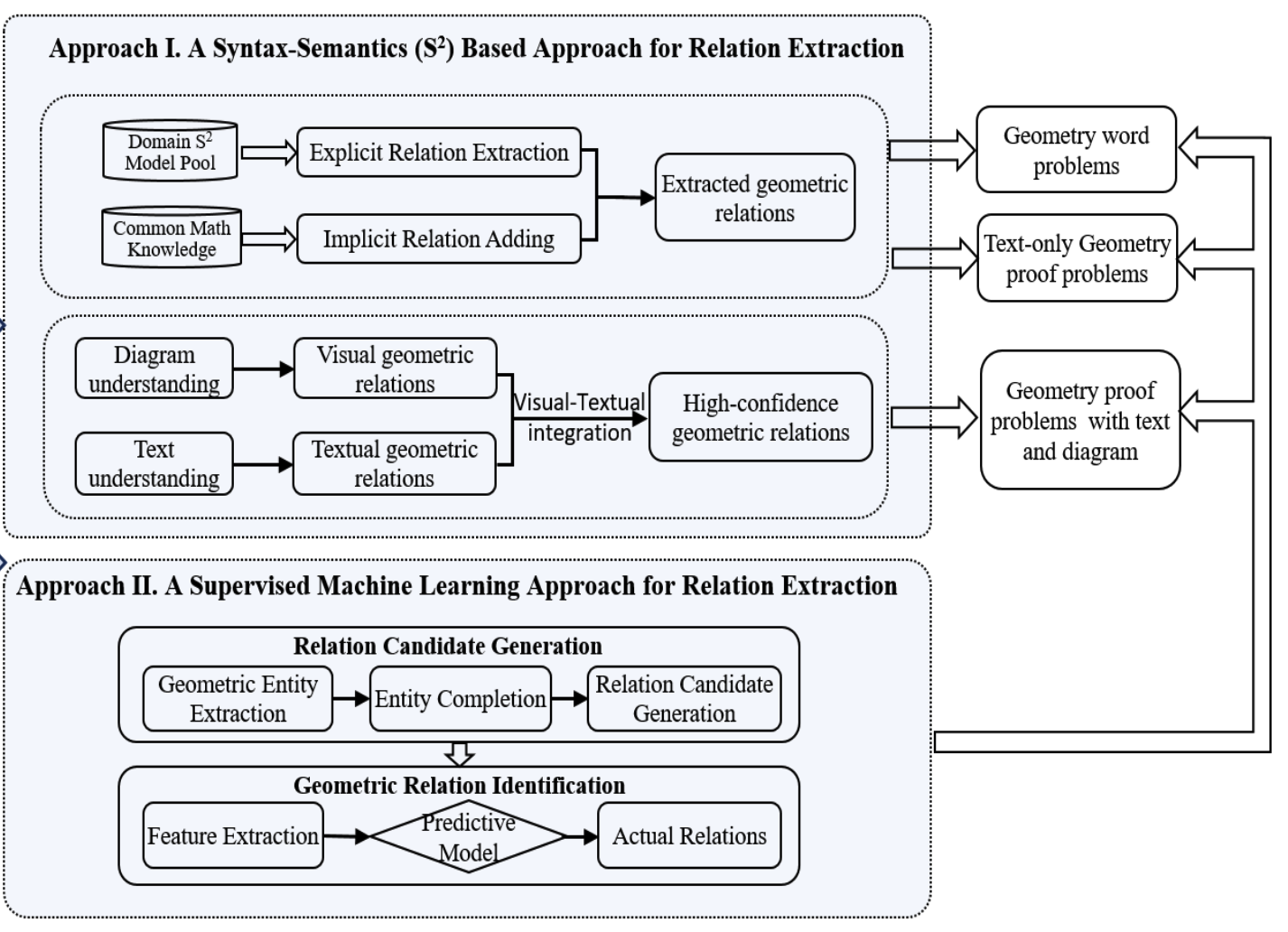
Prior Knowledge-driven Relation Extraction for Solving Plane Geometry Problems Stated by Text and Diagram
Introduction: We proposed an algorithm for proving plane geometry theorems stated by text and diagram in a complementary way. The problem of proving plane geometry theorems involves two challenging subtasks, being theorem understanding and theorem proving. This paper proposes to consider theorem understanding as a problem of extracting relations from text and diagram. A syntax–semantics (S2) model method is proposed to extract the geometric relations from theorem text, and a diagram mining method is proposed to extract geometry relations from diagram. Then, a procedure is developed to obtain a set of relations that is consistent with the given theorem with high confidence. Finally, theorem proving is conducted by using the deductive reasoning methods which take the extracted geometric relations as input. The experimental results show that the proposed theorem proving algorithm can prove 86% of plane geometry theorems in the test dataset of 200 theorems, which is all the theorems in the popular textbook. The proposed algorithm outperforms the existing algorithms mainly because it can extract relations not only from text but also from diagram.
[Keywords]: Geometry theorem proving, theorem understanding, relation extraction, syntax–semantics model, diagram mining.
Wenbin Gan, Xinguo Yu, Ting Zhang, and Mingshu Wang. Automatically proving plane geometry theorems stated by text and diagram. International Journal of Pattern Recognition and Artificial Intelligence, volume 33, page 1940003. World Scientific, 2019.
Wenbin Gan, Xinguo Yu, Chao Sun, Bin He, and Mingshu Wang. Understanding plane geometry problems by integrating relations extracted from text and diagram. In Pacific-Rim Symposium on Image and Video Technology (PSIVT), pages 366–381. Springer, 2017.
Wenbin Gan, Xinguo Yu, Sichao Lai, and Lei Xiang. Plane geometry diagram retrieval by using hierarchical searching strategy. In Proceedings of the International Conference on Internet Multimedia Computing and Service (ICIMCS), pages 201–206, 2016.
Xinguo Yu, Wenbin Gan, Danfeng Yang, and Sichao Lai. Automatic reconstruction of plane geometry figures in documents. In 2015 International Conference of Educational Innovation through Technology (EITT), pages 46–50. IEEE, 2015.
Automatic Understanding and Formalization of Plane Geometry Proving Problems in Natural Language
Introduction: Automatically understanding natural language problems is a long-standing challenging research problem in automatic solving. This work models the understanding of geometry problems as a problem of relation extraction, instead of as the problem of semantic understanding of natural language. Then it further proposes a supervised machine learning method to extract geometric relations, targeting to produce a group of relations to represent the given geometry problem. This method identifies the actual geometric relations from the relation candidates using a classifier trained from the labelled examples. The formalized geometric relations can then be transformed into the target system-native representations for manipulation in various tasks. Experiments conducted on the test problem dataset show that the proposed method can extract geometric relations at high F1 scores. The comparisons also demonstrate that the proposed method can achieve good performance against the baseline methods. Integrating the automatic understanding method with different geometry systems will greatly enhance the efficiency and intelligence in geometry tutoring.
[Keywords]: Understanding geometry problems, formalized geometric propositions, relation extraction, automatic solving, relation identification.
Wenbin Gan and Xinguo Yu. Automatic understanding and formalization of natural language geometry problems using syntax-semantics models. International Journal of Innovative Computing, Information and Control ICIC International, pages 83–98, 2018.
Wenbin Gan, Xinguo Yu, and Mingshu Wang. Automatic understanding and formalization of plane geometry proving problems in natural language: a supervised approach. International Journal on Artificial Intelligence Tools, volume 28, page 1940003. World Scientific, 2019.
